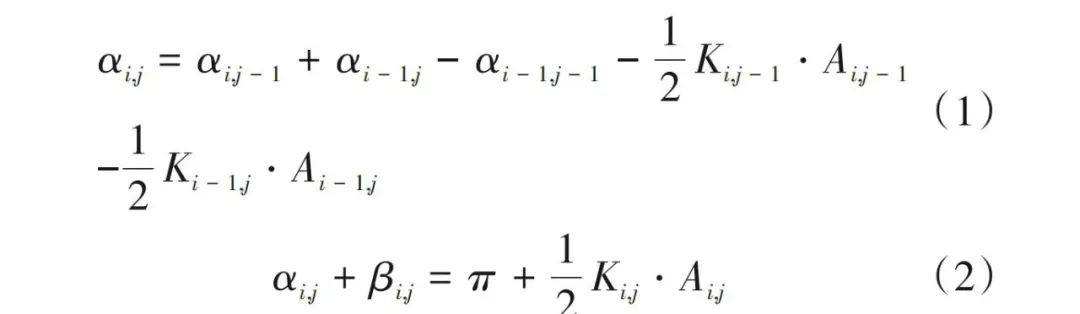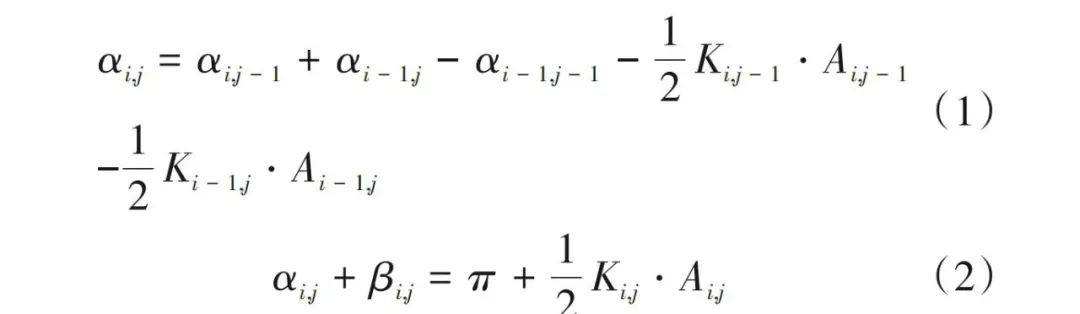根據樹脂基體類型的不同�,連續纖維增強樹脂基復合材料可分為熱固性(CFRTS)和熱塑性(CFRTP)兩種�����。相比前者,CFRTP 具有成型周期短�����、預浸料存儲條件簡單且保質期長�����、易于回收等優點 �。
當前CFRTP成型工藝類型主要有熱壓���、樹脂傳遞模塑成型(T-RTM)���、拉擠�����、纏繞和自動鋪放等�, 其中熱壓成型是以熱塑復合材料預浸料或層合板為原材料�,經加熱軟化后在模具中快速熱壓成型,而T-RTM 需要將干纖維預先鋪覆到模具中,然后進行注膠、加熱���,樹脂固結成型。
上述過程中軟化材料的熱變形-固結行為以及纖維鋪覆預成型的質量會對最終構件的力學性能�、尺寸精度和缺陷產生決定性影響�。與傳統短纖�����、長纖增強熱塑性復合材料的成型工藝相比���,由于連續纖維變形延展性不足���、樹脂流變行為復雜等因素,CFRTP 的鋪覆預成型和熱壓熱成 型階段會涉及復雜的變形機理�����,并導致一些典型缺陷�����,如翹曲�、褶皺�,甚至纖維斷裂等。而國內外大多仍然采用昂貴的“試錯”實驗進行產品開發�����,缺乏有效的理論模型開展工藝及性能預測研究�,嚴重影響產品質量、研發周期和推廣應用�����,因此開展有關 CFRTP成型過程仿真研究�����,準確預測纖維變形���、缺陷產生和殘余變形等行為�����,對于優化CFRTP成型工藝, 提高制品質量具有重要意義���。
當前用于CFRTP成型仿真的方法大體上可以分為兩類:運動學法與力學法�����。本文將評述各種模擬仿真方法的發展歷程及近年來最新研究成果���。
運動學法也被稱為映射法���、漁網算法或銷釘連接法(pin-jointed net)���,基本原理是利用幾何投影的方法���,將二維平面的織物投影至三維曲面表面�����。C. Mack 最早建立了映射法的雛形�,他忽略了紗線伸長和滑移帶來的影響�,推導出了可預測可展曲面鋪覆效果的微分方程,并通過對球面進行鋪覆實驗�����, 驗證了該方程���。后續學者對于運動學法鋪覆變形的完善與拓展�����,普遍基于該模型�����。Van Der WEE?N 認為織物節點間的紗線投影到三維曲面上是測地線���, 研究了曲面上測地線的解法�����。BOROUCHAKI等提出了一種新的運動學模擬算法�����,該算法考慮了繪制 在表面上的織物網格單元的真實幾何形狀。這樣的織物網格單元由曲線四邊形定義,該四邊形的邊緣是繪制在待鋪覆表面上具有相同長度的測地線。楊波等提出了一種基于幾何信息的映射算法�,該算法利用了相鄰節點處的曲率及切向量���,確定該節點的位置�����,避免了高強度的迭代計算,提高了仿真效率���。KAUFMANN 等利用運動學法與其建立的鋪覆數據庫結合,從纖維角度偏差�����、余料和材料剪切角度等方面評估仿真種子點和參考角的組合�����,試圖在部件的結構性能和制造成本之間找到平衡�����。
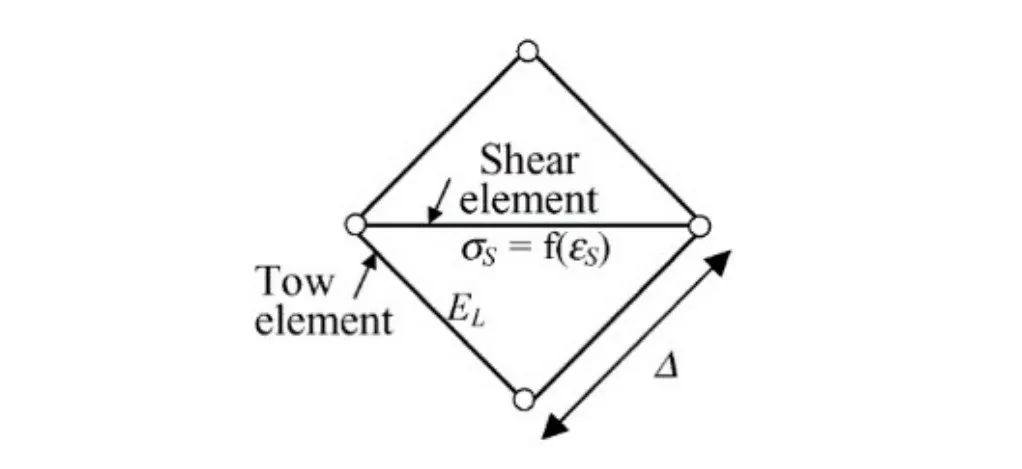
也有研究者另辟蹊徑�����,將運動學法與力學法相結合���。SHARMA等?提出了一種簡化的有限元模型 來模擬鋪覆過程�����,其單胞模型如圖1所示���。
Fig. 1 Unit cell model of Sharma
該單胞由銷釘連接的剛性桁架網絡組成�,通過對角單元引入剪切剛度�����,材料屬性可從拉伸試驗獲取�。該單元模型能夠代表平面內力對剪切變形和纖維滑移的影響���,同時作者預測該模型也適用于預浸料�,因為該模型可以考慮結合預浸料的剪切響應進 行模擬。運動學法極大地提高了計算效率���,然而這種模 型做出的假設條件過于理想,未考慮載荷、邊界條件 以及材料與模具之間的摩擦�,缺乏預測褶皺的能力���。
因此�����,運動學法主要應用于預浸料的手工鋪層與純纖維織物鋪覆性研究���,或者在初步的設計階段�����,對最終的成型效果做簡單預估�。
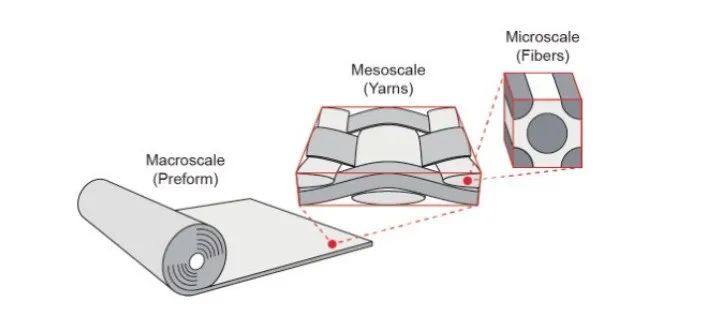
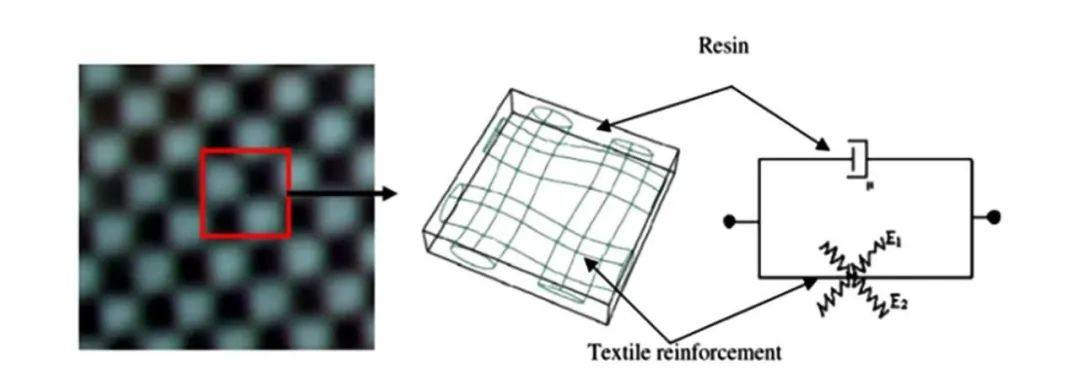
與運動學法相比�,力學法有限元模擬仿真考慮了復合材料的力學性能,并且可以與成型的物理過程相耦合�����。用于模擬CFRTP熱成型的力學模擬方法可分為三種:連續法�����、離散法以及半離散法�����。每種力學法耗費的計算成本差別很大,連續法成本最低�,而離散法最為昂貴�,半離散法介于兩者之間�����。連續法適用于宏觀現象的模擬和全結構問題的計算���,離散法適用于模擬介觀尺度與微觀尺度的現象�����,而半離散法因其特性對所有尺度均可適用�����。圖2 顯示了織物復合材料的三種不同的等級尺度�。
Fig. 2 Hierarchical scales for textile reinforcement materials
連續法是在復合材料連續介質力學的大框架下�����,假設復合材料是一個均質化的連續體���,這是目前為止研究最為廣泛的方法�。因為該模型僅在材料行為方面與經典連續結構有所不同�����,所以對各類結構具有良好的適用性�����。連續法模擬仿真分析本質上 是金屬成形仿真過程中深拉伸的一種拓展�,可采用 經典有限元軟件實現���。
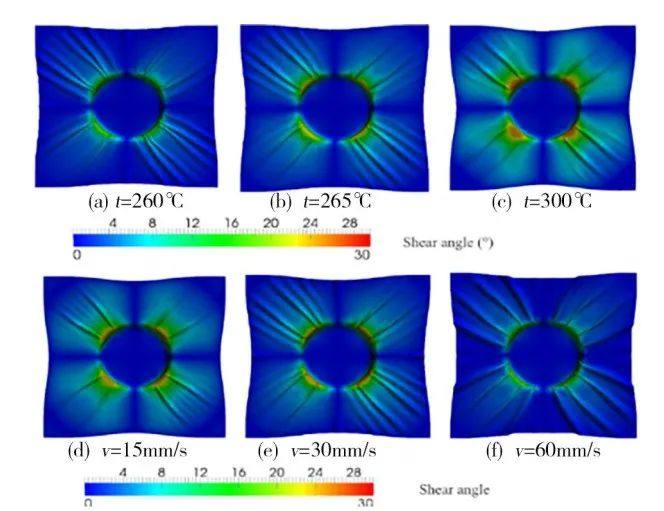
早期的連續法建模���,采用了理想化的纖維增強體模型�,假設單向或織物預浸料中的纖維為剛體,因此早期研究局限于成型主要的變形模式—面內剪切�����。如 HSIAO 等基于均質化假設�,假設在黏性樹脂流體中的是剛性纖維���,對熱成型過程進行了數值 模擬�,所提出的各向異性材料參數與溫度有關。該模型既能計算纖維取向���,又能計算冷卻階段產生的殘余應力。然而�,理想化的纖維增強模型不僅給后續的二次開發帶來困難�,也難以提高仿真精度���。此后隨著研究者進一步改良與有限元仿真技術發展���, 逐漸解決了有限元編程困難的問題���。YU 等提出了一種新的描述大變形下非正交材料行為的本構模型�����,旨在更好地表征獨立于網格剪切的面內正應變���。該模型能準確捕捉材料在不同加載路徑下的響應�, 真實地反映復合材料中纖維重分布和 重定向���。Guzman-Maldonado等基于麥克斯韋流變模型的推廣建立了一個非線性粘-超彈性模型�����,該模型是通過迭代的熱分析和成型分析來實現的,保證了沖壓變形和溫度場之間的耦合�����。計算得到的剪切角與實驗結果吻合較好���,其模型的仿真結果如圖3所示�����。結果表明�,在成型過程中溫度場發生了明顯的變化�����,單胞變形和模具接觸改變了局部熱性能和溫度���,而由于溫度變化和高應變率�����,面內剪切剛度增加,導致了頻繁起皺�����。在實際的熱成型過程中,溫度對預浸料的機械性能有著極大的影響���,由此可見熱力耦合模型對于提高CFRTP的熱成型仿真精度是不可或缺的。
Fig. 3 Simulation of a cylindrical forming at different?temperatures and different punch displacements rates
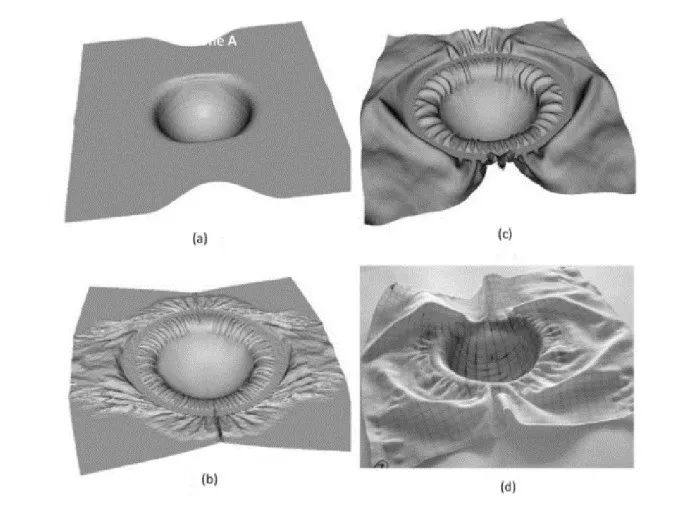
隨著近年來研究者們證明了彎曲剛度對缺陷褶 皺產生有著不可忽視的影響�����,尤其是在確定褶皺的形狀和大小方面之后���,不少研究者都將彎曲剛度納入了本構模型�����。考慮了彎曲剛度的本構模型�, 仿真將更貼合實際情況���,如圖4所示�����。
DOMINIK 等基于沃伊特-開爾文模型和廣義麥克斯韋模型提出了一種模擬單向或織物增強體的應變速率彎曲行為模型,該模型考慮了平面剪切�����、拉伸�����、彎曲剛度等力學行為���。根據熱塑性復合材料單向帶在加工條件下的熱表征結果�,成功地對所提出的黏彈性模型進行了參數化�。研究表明,廣義麥克斯韋方法結合非線性粘彈性行為最適合預測褶皺的產生及發展過程�。
Fig. 4 Hemispherical forming of an unbalanced textile?reinforcement
在研究某些特定問題時���,除了考慮面內剪切�����、拉伸���、彎曲剛度等常用的力學行為之外�,還會考慮其他力學因素,如 SOULAT 等研究成型過程中的孔隙率問題時�����,為了避免在實際成型仿真過程中對層合板每層進行單獨計算�����,開發了一種具有橫向應力的殼單元���,該殼單元增加了一個自由度�����,允許單元模擬厚度的變化,通過解耦彎曲和收縮應變來避免體積鎖定現象。結果表明,所獲得的橫向正應力與去除孔隙的結果非常吻合�。?
總體而言���,考慮的力學行為越多�,仿真模擬得到的結果會越接近實際情況���,然而現實中我們卻不得不考慮計算成本�,所以根據研究問題的實際需要,對力學行為進行取舍�����,可以忽略對最終結果影響小的力學行為以提高計算效率。連續法建模時由于假設連續介質代替了連續纖維,在這種情況下���,建模的困難之處在于宏觀模型必須考慮到纖維材料的異質 性�����,特別是在纖維大變形情況下�,否則仿真結果與實驗結果將出現較大的偏差�����。因此�����,連續法要用相對復雜的計算策略來設置單元中的纖維方向。
離散法將纖維增強相在介觀尺度下看作一系列的離散單元,該方法下的有限元模型由桁架、梁、殼或膜的網格單元組成。相比于連續法�����,這種模型的主要優點是直接考慮了材料的異質性�����,不需要復雜的計算策略來設置單元中的纖維方向�����,即可很清晰地描述纖維增強體內部結構。
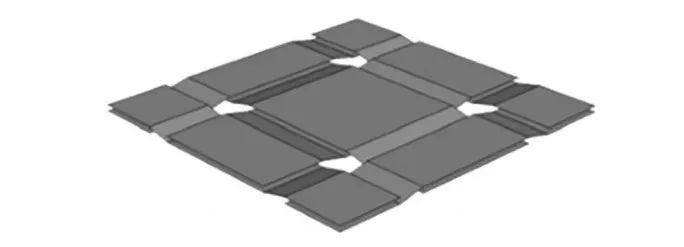
一般情況下�����,使用離散模型來模擬復合材料成型過程的研究目的是預測無褶皺成型結構�����,最基本的模型僅考慮了變形過程中纖維方向的計算。例如SIDHU 等提出了一種棋盤模型�����,該模型使用三維桁架單元和三維殼單元來模擬織物復合材料預制體 的成型���,其模型單胞如圖5所示�����。
Fig. 5 The unit cell for the checkerboard model
該模型考慮了纖維間摩擦�����、絲束干擾和纖維滑移�。結果表明�����,大變形過程中隨著剪切角的變化���,紗線間出現明顯的滑移�����。JAUFFRèS 等提出了一種基于亞彈性描述的顯式有限元公式離散模型�,紗線的拉伸行為由桁架�����、梁等一維單元模擬�,織物的剪切行為由殼或薄膜單元模擬�����,該模型有限元分析結果與實驗數據基本一致�。SHERWOOD 等在該模型的框架下�����,考慮了復合材料熱沖壓過程中模具與織物之間摩擦�,使用恒定和可變摩擦因數做對比實驗�, 進行半球沖壓模擬。結果表明提高沖壓速度會導致 模具與織物界面的摩擦力增加�����,從而增加了纖維的拉伸應力�����,且沖壓力與沖壓速度無關�����。HARRISON 等提出了一個多尺度能量模型,使用桁架和殼單元來模擬黏性織物復合材料的熱成型,通過將多尺度能量模型與宏觀尺度模型相結合,使得該模型能夠預測復合材料成型過程中的剪切應力-剪切角-剪 切速率行為,適用于在不同剪切速率下的成型模擬�����。
此外���,離散法的特性允許模型更容易預測一些細觀現象���,如 BOISSE 等基于纖維增強體離散模型的宏觀成型�,預測了纖維之間的大滑移現象�。在該模型中每個織物單元被模擬為一組非常簡化的殼單元,在保證自由度很低的情況下,還能描述纖維之 間的摩擦接觸,如圖6所示���。
Fig. 6 Simplified finite-element model of the woven unit cell
離散法所耗費的計算資源巨大,計算效率低,RAMGULAM等[31]認為,雖然詳細的有限元分析對最終方案必不可少,但近似的力分析有利于在工藝優化過程中快速篩選大量的鋪層方案�。因此�,他提出了一種快速計算織物褶皺的近似力學分析方法�����。利用一種基于微分幾何的鋪覆算法���,如公式(1)、(2)所示�����,獲得了織物在曲面上變形后的紗線取向�����。
式中���,K 是高斯曲率,α�、β 為織物內角。通過調整外部載荷和給定織物的剪切性能�,可以快速確定織物鋪覆時出現問題的區域���。此外,壓力分布可用于計算層間摩擦力���。這種計算效率高的力/褶皺方法還可用于擴展運動學褶皺模型的能力�����,以補充全尺度有限元分析。
離散法主要的局限性在于因為將每根纖維看作獨立單元���,所以必須考慮大量纖維復雜的機械性能以及它們之間的相互作用���,且平面內剪切和拉伸之間是相互依賴的�����,很難考慮剛度之間的耦合。離散法通常只用在介觀尺度上分析小數量的單元�,并且 這個級別一般不適合分析整個成型模擬過程�����。因 此�,離散法建模時需要在單胞模型的準確性和自由度總數之間進行折中�。單胞的建模必須足夠準確才能獲得正確的整體宏觀力學行為,且每個單胞的自由度數要盡量小�����,以便計算成千上萬個單胞的成型過程�����。
半離散法是在介觀尺度上構建的特定有限元�。一方面,與離散法一樣�����,材料的力學行為被拆分���,僅考慮主要剛度(如拉伸�����、面內剪切或面外彎曲)�;另一方面�,用與連續法相同的方式,將所有剛度都視為在半離散單元內部�,可以很容易地將剛度參數傳遞到 宏觀模型的半離散單元中���。
HAMILA 等提出了一種考慮拉伸和面內剪切行為的三結點單元�����。經紗和緯紗方向相對于單元側面是任意的�����,材料參數是通過標準拉伸和偏軸拉伸試驗確定。而后續 HAMILA等改良了這種半離散三角形單元�����,除了考慮拉伸剛度和平面內剪切剛度之外���,還考慮了彎曲剛度�。彎曲行為由懸臂彎曲試驗給出,半離散單元的彎曲曲率由相鄰單元的位移得到�,就鋪覆過程中褶皺的出現和發展分析了所考慮的三種剛度的影響。CHEN 等集中研究了熱成型過程中 CFRTP 的層間剪切行為,提出了一種層合板粘彈性模型,其模型示意如圖7所示�。該模型應用了具有八個節點的大位移三維內聚單元�����,研究織物熱塑性復合材料的層間剪切機理。模型考慮了不同加工溫度和不同應變速率下的拉伸���、壓縮和面內剪切行為。通過該模型�,可以模擬溫度對應變率的影響規律�����。WANG等在該模型的基礎上考慮了熔點附近不同溫度下鋪層的張力、面內剪切和彎曲剛度�����, 模擬了多層 CFRTP 熱成型過程中的接觸摩擦�����,并使 用拉格朗日乘子法進行計算�����,仿真得到的成型剪切角和起皺角與熱成型實驗結果吻合較好。
Fig. 7 Visco-elastic model for laminates
半離散法旨在避免使用應力張量,僅通過張力以及面內剪切和彎曲剛度直接定義單元上的載荷�。這些量簡單地定義在一個單胞上�����,而且這些材料參數可以通過復合材料的標準測試直接獲得。半離散法也可以與經典有限元技術一起使用�����,并且通過對 特定有限元單元進行定義考慮纖維的異質性���,進而提高計算精度�����。
目前,在 CFRTP 成型模擬仿真領域仍存在一些重要的科學問題有待解決�����,例如沒有一種較為系統的流固熱力耦合分析模型�����,缺少針對成型缺陷成因機理的探索�,只是簡單的定性分析�。同時,在介觀與宏觀尺度建模的相關文獻中可以看出���,開發一個同步的多尺度模型來模擬仿真成型過程仍然是一個巨大挑戰���。?
總體而言���,我國 CFRTP 成型的模擬仿真仍停留在實驗室階段�����,尚不能夠滿足實際生產的需求。為了解決高性能CFRTP大批量生產所需求的高效低成本�����、穩定可靠的制造工藝���,對CFRTP成型的模擬仿真依然是未來樹脂基復合材料領域的重要研究方向之 一,值得進一步深入研究�。
毛晉軒,劉東,史鵬程等.連續纖維熱塑性復合材料熱成型仿真研究[J].宇航材料工藝,2022,52(04):21-26.
原文始發于微信公眾號(艾邦復合材料網):連續纖維熱塑性復合材料熱成型模擬仿真方法及其發展趨勢